Ở bài viết này, VerbaLearn sẽ giúp bạn đọc tìm hiểu tổng quan lý thuyết phép quay và một số dạng bài tập đặc trưng theo chương trình toán 11.

Định nghĩa phép quay
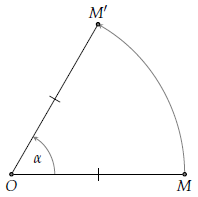
Cho điểm O và góc lượng giác α. Phép biến hình biến O thành chính nó, biến mỗi điểm M khác O thành điểm M sao cho OM’ = OM và góc lượng giác (OM; OM’) bằng α được gọi là phép quay tâm O góc quay α.
Điểm O gọi là tâm quay, α gọi là góc quay. Phép quay tâm O góc α, kí hiệu là Q(O;α).
+) Phép quay nào biến là cờ (C) thành lá cờ (C’):
+) Phép quay nào biến là cờ (C’) thành lá cờ (C):
Tính chất phép quay
1. Phép tịnh tiến là phép biến hình biến
+) Bảo toàn khoảng cách giữa hai điểm bất kì.
+) Biến một đường thẳng thành một đường thẳng.
+) Biến một đoạn thẳng thành một đoạn thẳng bằng đoạn thẳng đã cho.
+) Biến một tam giác thành một tam giác bằng tam giác đã cho.
+) Bien một đường tròn thành một đường tròn có cùng bán kính.
Giả sử quay tâm O góc quay α biến đường thẳng d thành đường thẳng d’. Khi đó:
+) Nếu thì góc giữa d và d’ bằng α.
+) Nếu thì góc giữa d và d’ bằng π – α.
2. Hai hình bằng nhau
Hai hình được gọi là bằng nhau nếu có phép dời hình biến hình này thành hình kia.
Dạng 1: Tìm tọa độ ảnh của một điểm qua phép quay
Phương pháp giải
Phương pháp 1: Sử dụng định nghĩa
Trong mặt phẳng tọa độ Oxy, gọi M’(xM, yM) là ảnh của M(xM, yM) qua phép quay tâm I(a,b), góc quay α. Khi đó:
Từ (1), sử dụng công thức tính độ dài, sẽ tìm được phương trình thứ nhất theo hai ẩn
Từ (2), sử dụng định lý hàm số cos, sẽ tìm được phương trình thứ hai theo hai ẩn.
Giải hệ phương trình này tìm được xM, yM, từ đó suy ra tọa độ M’(xM, yM).
Chú ý góc của phép quay để chọn được tọa độ điểm phù hợp
Phương pháp 2: Sử dụng công thức tọa độ
Phương pháp 3: Trong các trường hợp đơn giản sử dụng hệ trục tọa độ, thực hiện phép quay tìm ngay được tọa độ điểm ảnh.
Bài tập vận dụng
Câu 1. Trong mặt phẳng tọa độ Oxy, tìm tọa độ A’, B’ lần lượt là ảnh của A, B quay phép quay tâm O, góc quay 90°. Biết
a) A(1; 0)
ĐS: A’(0; 1)
b) B(0; −2)
ĐS: B’(2; 0)
Lời giải
a) Xét điểm A(1; 0)
Gọi A’ có tọa độ là (x’; y’). Khi đó:
Từ (1), suy ra (x’)2 + (y’)2 = 1
Từ (2), suy ra 1.x2 + 0.y2 = 0
Vậy thu được (x’; y’) = (0; 1) hoặc (x’; y’) = (0; −1). Vì góc quay dương nên thu được điểm A’ (0; 1)
b) Xét điểm B(0; −2)
Gọi B’có tọa độ là (x’; y’). Khi đó:
Biểu diễn điểm A, B trên hệ trục tọa độ, có thể suy ra ngay tọa độ điểm A’ và B’.
Câu 2. Trong mặt phẳng Oxy, cho tam giác ABC có A(1; 1), B(0; 5), C(−2; −1) và đường thẳng d: 2x − y − 4 = 0. Hãy xác định tọa độ các đỉnh của tam giác A’B’C’ và phương trình đường thẳng d theo thứ tự là ảnh của tam giác ABC và đường thẳng d qua phép quay tâm O, góc quay 90◦.
Lời giải.
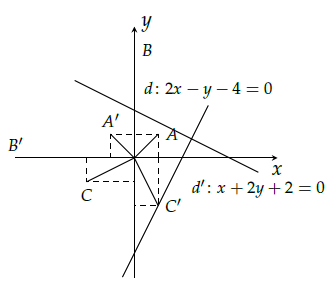
Phép quay tâm O, góc quay 90°:
+) Biến A(1; 1) thành A’(−1; 1),
+) Biến B(0; 5) thành B’(−5; 0),
+) Biến C(−2; −1) thành C’(1; −2).
Phép quay tâm O, góc quay 90° biến đường thẳng d: 2x − y − 4 = 0 thành đường thẳng d’: x + 2y + 2 = 0.
Câu 3. Trong mặt phẳng tọa độ Oxy cho điểm A(2; 0) và đường thẳng d: x + y − 2 = 0. Tìm ảnh của A và d qua phép quay tâm O góc 90°.
Lời giải.
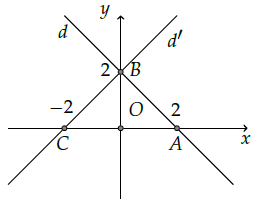
Ta có: Q(O,90°) (A) = B với B(0; 2).
Q(O,90°) (B) = C với C(−2; 0).
Gọi d’ là ảnh của d qua Q(O,90°). Vì A, B thuộc d nên B, C thuộc d’.
Phương trình đường thẳng d’: x − y + 2 = 0.
Dạng 2. Tìm phương trình ảnh của một đường tròn qua phép quay
Phương pháp giải
Vì phép quay biến đường tròn thành đường tròn có cùng bán kính nên để tìm phương trình ảnh của đường tròn qua phép quay, chúng ta thực hiện qua ba bước sau đây:
+) Xác định tọa độ tâm I và bán kính R của đường tròn tạo ảnh từ phương trình đường tròn đã cho
+) Tìm tọa độ tâm I’ là ảnh của tâm I quay phép quay
+) Viết phương trình đường tròn ảnh với tọa độ tâm I’ và bán kính R.
Bài tập vận dụng
Câu 1. Trong mặt phẳng tọa độ Oxy, hãy ảnh của đường tròn (C’) qua phép quay tâm O, góc quay α trong các trường hợp sau đây:
a) (C): (x − 2)2 + (y − 1)2 = 1, α = 90°
ĐS: (C’): (x + 1)2 + (y − 2)2 = 1
b) (C): x2 + y2 − 4x – 5 = 0, α = 90°
ĐS: (C’): x2 + (y – 2)2 = 9.
Lời giải
a) Ta có:
+) Tâm I(2; 1), R = 1. Suy ra: I’ (−1; 2), R’ = R = 1.
+) (C’): (x + 1)2 + (y − 2)2 = 1.
b) Ta có:
+) Tâm I(2; 0), R = 3. Suy ra: I’(0; 2), R’ = R = 3.
+) (C’): x2 + (y − 2)2 = 9.
Câu 2. Trong mặt phẳng tọa độ Oxy, hãy tìm ảnh của đường tròn (C’) qua phép quay tâm O, góc quay α trong các trường hợp sau đây:
a) (C): x2 + y2 − 2x + 4 = 1, α = −90°
ĐS: (C’): (x + 2)2 + (y + 1)2 = 6
b) (C): x2 + (y − 1)2 = 1, α = 60°.
ĐS: (C’):
Lời giải.
a) Ta có:
+) Tâm I(1; −2),
Suy ra: I’(−2; −1),
+) (C’): (x + 2)2 + (y + 1)2 = 6.
b) Ta có:
+) Tâm I(0; 1), R = 1.
Suy ra: , R’ = R = 1
+) (C’):
Câu 3. Trong mặt phẳng tọa độ Oxy, hãy tìm ảnh của đường tròn (C’) qua phép quay tâm O, góc quay α trong các trường hợp sau đây:
a) (C): x2 + y2 − 4x + 2y = 0, α = −30°.
ĐS: (C’):
b) (C): x2 + y2 + 6x + 5 = 0, α = 90◦.
ĐS: (C’): x2 + (y + 3)2 = 4
Câu 4. Trong mặt phẳng tọa độ Oxy, hãy tìm ảnh của đường thẳng d qua phép quay tâm O, góc α trong các trường hợp sau đây
a) d: x + y − 2 = 0, α = 90◦;
ĐS: x − y + 2 = 0
b) d: x − 3y + 11 = 0, α = −90◦;
ĐS: 3x + y − 11 = 0
c) d: x − 3y + 5 = 0, α = 60◦;
ĐS:
d) d: 2x − y + 6 = 0, α = 45◦.
ĐS:
Lời giải.
a) Lấy M(0; 2), N(2; 0) ∈
Gọi M’, N’ lần lượt là ảnh của M, N qua phép quay Q(O,90°).
Khi đó:
và
Suy ra: M’(−2; 0), N’(0; 2).
Gọi d’ là ảnh của d qua phép quay Q(O,90°), khi đó d’ đi qua M’, N’.
Ta có:
Suy ra phương trình đường thẳng d’ là 1(x − 0) − 1(y − 2) = 0 ⇔ x − y + 2 = 0.
b) Lấy M(−11; 0), N(1; 4) ∈
Gọi M’, N’ lần lượt là ảnh của M, N qua phép quay Q(O,−90°).
Khi đó:
và
Suy ra: M’(0; 11), N’(4; −1).
Gọi d’ là ảnh của d qua phép quay Q(O,−90°), khi đó d’ đi qua M’, N’.
Ta có:
Suy ra phương trình đường thẳng d’ là:
3(x − 0) + 1(y − 11) = 0 ⇔ 3x + y − 11 = 0.
c) Lấy M(−5; 0), N(1; 2) ∈
Gọi M’, N’ lần lượt là ảnh của M, N qua phép quay Q(O,60°).
Khi đó:
và
Suy ra:
Gọi d’ là ảnh của d qua phép quay Q(O,60°), khi đó d’ đi qua M’, N’.
Ta có:
Suy ra phương trình đường thẳng d’ là:
d) Lấy M(−3; 0), N(0; 6) ∈
Gọi M’, N’ lần lượt là ảnh của M, N qua phép quay Q(O,45°).
Khi đó:
và
Suy ra:
Gọi d’ là ảnh của d qua phép quay Q(O,45°), khi đó d’ đi qua M’, N’.
Ta có:
Suy ra phương trình đường thẳng d’ là:
Câu 5. Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 2x − 3y + 2 = 0 và đường tròn có phương trình là (C): x2 + y2 − 4x − 4y − 1 = 0.
a) Viết phương trình d’ là ảnh của d qua phép Q(O,90°).
ĐS: 3x + 2y + 2 = 0
b) Viết phương trình (C’) là ảnh của (C) qua phép Q(O,90°).
ĐS: (x + 2)2 + (y − 2)2 = 9
Lời giải.
a) Lấy M(−1; 0), N(2; 2) ∈
Gọi M’, N’ lần lượt là ảnh của M, N qua phép quay Q(O,90°).
Khi đó:
và
Suy ra M’(0; −1), N’(−2; 2).
Gọi d’ là ảnh của d qua phép quay Q(O; 90°), khi đó d’ đi qua M’, N’.
Ta có:
Suy ra phương trình đường thẳng d’ là:
3(x − 0) + 2(y + 1) = 0 ⇔ 3x + 2y + 2 = 0
b) Đường tròn (C) có tâm I(2; 2), bán kính R = 3.
Gọi I’ là ảnh của I qua phép quay Q(O,90°).
Khi đó:
Suy ra: I’(−2; 2).
Vì (C’) là ảnh của (C) qua phép quay Q(O,90°) nên (C’) có tâm là I’ và bán kính bằng 3.
Vậy (C’): (x + 2)2 + (y − 2)2 = 9.
Câu 6. Trong mặt phẳng tọa độ Oxy, cho điểm M(2; 2), đường thẳng d: 2x − y − 2 = 0 và đường tròn (C): (x − 1)2 + (y − 1)2 = 4. Tìm ảnh của M, d, (C) qua:
a) Phép quay tâm O góc quay 45°.
ĐS: , d’:
, (C’): x2 + (y − 2)2 = 4
b) Phép quay tâm I(1; 2) góc quay 45°.
ĐS: ; d”:
; (C”):
Lời giải.
a) Gọi M’ là ảnh của M qua phép quay Q(O,45°).
Khi đó:
Suy ra:
Lấy A(1; 0), B(0; −2) ∈ d.
Gọi A’, B’ lần lượt là ảnh của A, B qua phép quay Q(O,45°).
Khi đó:
và
Suy ra:
Gọi d’ là ảnh của d qua phép quay Q(O,45°), khi đó d’ đi qua A’, B’.
Ta có:
Suy ra phương trình đường thẳng d’ là
Đường tròn (C) có tâm E(1; 1), bán kính R = 2.
Gọi E’ là ảnh của E qua phép quay Q(O,45°).
Khi đó:
Suy ra:
Gọi (C’) là ảnh của (C) qua phép quay Q(O,45°) nên (C’) có tâm là E’ và bán kính bằng 2.
Vậy (C’): x2 + (y − 2)2 = 4.
b) Gọi M’ là ảnh của M qua phép quay Q(I,45°).
Khi đó:
Suy ra:
Lấy A(1; 0), B(0; −2) ∈ d.
Gọi A”, B” lần lượt là ảnh của A, B qua phép quay Q(I,45°).
Khi đó:
và
Suy ra:
Gọi d” là ảnh của d qua phép quay Q(I,45°), khi đó d” đi qua A”, B”.
Ta có:
Suy ra phương trình đường thẳng d” là:
Đường tròn (C) có tâm E(1; 1), bán kính R = 2.
Gọi E” là ảnh của E qua phép quay Q(I,45°).
Khi đó:
Suy ra:
Gọi (C”) là ảnh của (C) qua phép quay Q(I,45°) nên (C”) có tâm là E” và bán kính bằng 2.
Vậy (C”):
Câu 7. Trong mặt phẳng Oxy, cho điểm A(4; 3), đường tròn (C): . Tìm ảnh của A, (C) qua phép quay tâm O góc quay 60°.
ĐS: ; (C’):
Lời giải.
Gọi A’ là ảnh của A qua phép quay Q(O,60°).
Khi đó:
Suy ra:
Đường tròn (C) có tâm , bán kính
. Gọi E’ là ảnh của E qua phép quay Q(O,60°).
Khi đó:
Suy ra:
Gọi (C’) là ảnh của (C) qua phép quay Q(O,60°) nên (C’) có tâm là E’ và bán kính bằng
Vậy (C’):
Câu 8. Cho tam giác ABC có các đinh kí hiệu theo hướng âm, dựng bên ngoài các hình vuông ABDE, BCKF. Gọi P là trung điểm của AC, H là điểm đối xứng của D qua B, M là trung điểm của FH.
a) Xác đinh ảnh của trong phép quay Q(B,90°).
ĐS:
b) Chứng minh DF = 2BP và DF ⊥
Lời giải.
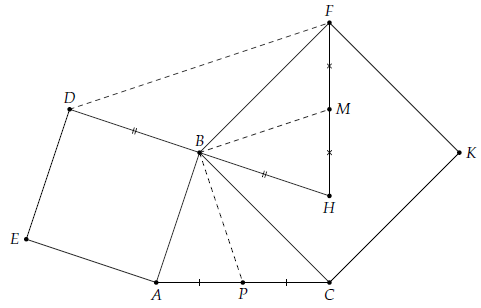
a) Từ giả thiết ta có:
b) Vì
Nên ta có:
Mà: BM là đường trung bình của tam giác HFD
Nên: DF = 2BP và DF ⊥ BP.
Câu 9. Cho tam giác ABC. Dựng về phía ngoài tam giác đó các tam giác BAE và CAF vuông cân A. Gọi I, M, J theo thứ tự là trung điểm của EB, BC, CF. Chúng minh tam giác IMJ vuông cân.
Lời giải.
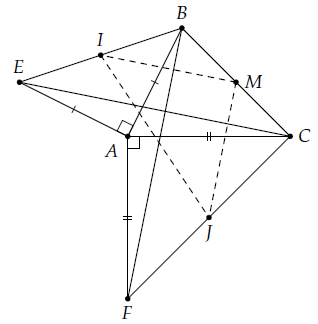
Vì ∆ABE, ∆ACF là những tam giác vuông cân tại A nên ta có:
Suy ra:
Mà: MI, MJ lần lượt là đường trung bình của ∆BEC, ∆CBF nên
Do đó: ∆IMJ vuông cân tại M
Câu 10. Cho ba điểm A, B, C thẳng hàng theo thứ tự. Lấy các đoạn thẳng AB, BC làm cạnh, dựng các tam giác đều ABE và BCF nằm cùng về một phía so với đường thẳng AB. Gọi M, N lần lượt là trung điểm của các đoạn thẳng AF và CE. Chứng minh tam giác BMN đều.
Lời giải.
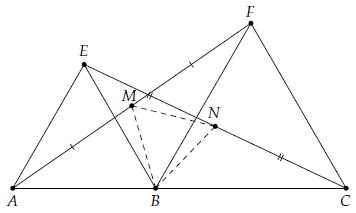
Vì tam giác ABE và BCF là những tam giác đều nên ta có
(Vì M, N lần lượt là trung điểm của AF, CE)
Do đó: hay tam giác BMN đều.